la méthode de Dichotomie
Dans ce TP, nous nous intéressons à la résolution numérique
des équations non linéaires de type f (x) = 0 ou g(x) = x, où f et g sont des
fonctions non linéaires. Pour résoudre ce type de problème, deux méthodes sont utilisées :
– La méthode de
dichotomie (résolution d’équations du type f (x) = 0).
– La méthode de
Newton (résolution d’équations du type f (x) = 0)
Toutes ces méthodes sont des méthodes itératives
|
Principe de la méthode
de Dichotomie
|
|
Certaines
équations ne pouvant pas être résolues algébriquement, on peut néanmoins
trouver les valeurs approchées des solutions.
|
|
Supposons
que l'équation f(x)= l admette une solution unique asur l'intervalle [a ; b], et l'on
veuille une valeur approchée de cette solution à 10-p près,
La fonction f est strictement monotone sur [a ; b], supposons par que f est
strictement croissante.
|
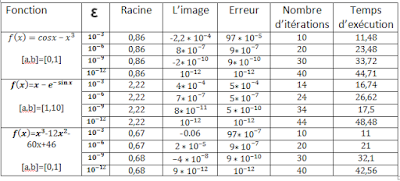
Programmation
de la méthode de dichotomie : ( en matlab )
% la méthode de dichotomi
clear all;
close all;
clc
tic;
f=inline('(x-(exp(sin(x))))');
d=iddinplutf(x);
%f=inline('cos(x)-x*3');
a=0;aa=a;
b=1;bb=b;
eps=1e-12;
err=1;
Iter=0;
while (err >= eps)
x0=(a+b)/2;
Iter=Iter +1;
if f(a)*f(x0)<0
b=x0;
err=abs(a-x0);
else
a=x0;
err=abs(b-x0);
end
fprintf('eps=%2.12f \t',eps);
fprintf('racine=%2.12f \t',x0);
fprintf('f(x0)=%2.12f \t',f(x0));
fprintf('erreur=%2.12f \t',err);
fprintf('Iter=%2.12f \t',Iter);
fprintf('\n');
fplot(f,[aa bb]);
hold all;
plot(x0,f(x0),'ro');
xlabel('x'),ylabel('f');
title(['iteration N°=',int2str(Iter),'x=',num2str(x0),]);
hold off;
grid on;
pause(1)
end
toc;